Spaghetti Accelerator 意大利面加速器

2. Spaghetti Accelerator 意大利面加速器#

2.1. Spaghetti Accelerator 意大利面加速器#

2.1.1. 题目#

When a piece of spaghetti is pushed into a bent tube, small debris of spaghetti may be ejected from the other end of the tube at a surprisingly high speed. Investigate this phenomenon.

2.1.2. 题目翻译#

当把一根意大利面推入一个弯曲的管子时，管子的另一端可能会以惊人的高速喷出小块的意大利面碎屑。研究这一现象。

2.1.3. 题目解析#

2.1.3.1. deepseek#

  • 引言

当一根意大利面被推入一个弯曲的管子时，管子的另一端可能会以惊人的高速喷出面条的碎屑。这一现象涉及流体力学、材料科学和力学等多个领域的原理。为了研究这一现象，我们可以将其分解为几个部分，逐步分析每个因素对结果的影响。 第一步：理解实验中的组成部分

  • 意大利面： 意大利面是由硬质小麦粉和水制成的圆柱形面食。它具有一定的脆性，当受到外力作用时容易断裂成小段。

  • 弯曲的管子： 弯曲的管子为意大利面的运动路径引入了曲率。这种弯曲会影响流体动力学特性以及意大利面与管子内壁的相互作用。

  • 第二步：分析意大利面与管子的相互作用

当意大利面被推入直管时，它会受到管子内壁的摩擦力。然而，在弯曲的管子中，由于曲率的存在，还会产生额外的力。

  • 摩擦力： 意大利面与管子内壁之间的摩擦力会阻碍其运动，导致面条弯曲并可能断裂。

  • 向心力： 当意大利面在弯曲部分移动时，向心力会使其压向管子的外侧壁，这会增加摩擦力和面条所受的应力。

  • 第三步：意大利面的应力与断裂

  • 摩擦力和向心力的共同作用会导致意大利面在某些部位产生应力集中，尤其是在与管子内壁接触的点。

  • 应力集中点：

    • 弯曲应力： 意大利面在弯曲部分会受到弯曲应力，这种应力可能导致面条断裂。

    • 剪切应力： 当面条被快速推入管子时，剪切应力也可能导致其断裂。

  • 第四步：碎屑的高速喷射机制

当意大利面在弯曲管子中断裂时，断裂的碎屑可能会被管内的空气压力或残余动能推动，从管子的另一端高速喷出。

  • 空气压缩效应： 如果管子内部存在空气，快速推动意大利面可能会压缩空气，形成局部高压区。当碎屑断裂时，压缩空气会迅速膨胀，推动碎屑高速喷出。

  • 动能传递： 意大利面在被推动时具有一定的动能。当面条断裂时，部分动能会传递给碎屑，使其以高速飞出。

  • 第五步：实验验证与参数影响

  • 为了进一步验证这一现象，可以通过实验研究以下参数的影响：

    • 管子的弯曲角度： 不同弯曲角度对意大利面断裂和碎屑喷射速度的影响。

    • 推动速度： 推动意大利面的速度是否会影响碎屑的喷射速度。

    • 管子的直径： 管子直径的变化是否会影响碎屑的喷射行为。

    • 意大利面的湿度： 面条的湿度可能影响其脆性和断裂方式。

  • 结论

意大利面在弯曲管子中被推动时，由于摩擦力和向心力的作用，面条容易在应力集中点断裂。断裂的碎屑在管内空气压缩效应和动能传递的作用下，可能会以高速从管子的另一端喷出。这一现象可以通过实验进一步验证，并研究不同参数对结果的影响。

2.1.4. 题目解析#

2.1.4.1. qwen#

这种现象可以通过流体力学和固体材料的力学行为来解释。当你将一根意大利面推入一个弯曲的管子时，由于意大利面与管壁之间的摩擦以及弯曲形状导致的空间限制，意大利面可能会断裂成小碎片。这些小碎片被后续推进的意大利面条推动并加速。

以下是详细的分析：

**摩擦力**的作用：当意大利面通过弯管时，它会受到来自管壁的摩擦阻力。这会导致意大利面**内部产生应力**，尤其是在弯曲的部分，因为这里的曲率增加了局部应力。

结构弱点：如果意大利面存在任何微小的缺陷或薄弱点，这些位置更容易发生断裂。一旦开始断裂，裂纹就会迅速扩展，因为进一步的推压会使断裂加剧。

压力积累与释放：随着更多的意大利面被推入管中，前面已经进入的小碎片会被压缩在一个相对封闭的空间内。这不仅增加了它们的速度，还可能使它们以较高的速度从另一端弹出，类似于气枪发射子弹的原理。

材料特性：意大利面是脆性材料，在受力不均匀的情况下容易断裂。其断裂后的碎片边缘可能非常锋利，能够以意想不到的速度被推出。

这个过程涉及了材料科学中的断裂力学、固体力学以及流体力学的基本原理。理解这一现象可以帮助我们更好地设计食品加工设备或者研究材料在受限空间内的行为特征。同时，这也提醒我们在处理类似操作时注意安全，避免因高速飞出的碎片造成伤害。

2.1.5. 题目解析#

2.1.5.1. chatgpt#

这个现象涉及流体力学、弹性力学和粉碎动力学等多个物理学领域。我们可以从以下几个方面分析该现象的可能机制：

  1. 斯帕盖蒂的断裂与碎片形成 意大利面（spaghetti）是一种脆性材料，在受力弯曲时容易断裂。其断裂行为受弯曲应力和脆性断裂力学影响：

当一根意大利面被推入弯曲的管道时，它会受到轴向推力和管壁的约束力，导致其弯曲和变形。 由于弯曲应力，意大利面可能会在某些应力集中的位置发生断裂，并产生细小碎片。 2. 弹性势能释放与碎片加速 断裂后的意大利面碎片可能会因弹性势能的释放被加速。 由于碎裂过程中，存储在意大利面的弹性能量会释放给碎片，使其以较高的速度被抛出。 这个效应类似于“鞭子效应”（whip effect），即在某些条件下，局部能量的快速释放会导致极端的速度变化。 3. 管道内的气体流动与碎片加速 意大利面的插入可能会压缩管道内的空气，导致管道内部形成短暂的高压区域。 当碎片断裂并释放时，管道内的空气可能会推动碎片，进一步加速其运动。 这种现象类似于气枪效应（airgun effect），即当气体突然释放时，可以对小物体施加很大的推力。 4. 摩擦力与边界效应 意大利面在管道内部受摩擦力作用，其断裂碎片可能会因管壁的约束而改变方向并加速。 若管壁存在某种微小的不规则性或曲率变化，碎片可能会沿着某些特定方向被引导出去，导致它们以高速射出。 实验验证与潜在应用 为了验证该现象，可以进行以下实验：

使用高速摄像机记录意大利面碎片的弹射过程，分析其速度和轨迹。 通过改变管道的弯曲半径和直径，研究这些因素对碎片弹射速度的影响。 在管道内引入不同的空气压力，观察是否存在明显的空气动力学加速效应。 这一现象不仅有趣，也可能对食品加工、粉碎机械、甚至弹射器或微颗粒动力学研究提供一定的启发

2.1.6. 题目解析#

2.1.6.1. gemini#

一个有趣的物理现象，涉及到多个方面的相互作用。下面我用中文分析一下这个现象：

  1. 力的传递与应力集中:

推力: 当我们推动意大利面条时，我们施加的力沿着意大利面条传递。由于意大利面条本身具有一定的柔韧性，它会发生弯曲。 应力集中: 弯曲处，尤其是弯曲角度较大的地方，会形成应力集中。这意味着，原本均匀分布的力，现在集中在弯曲的几个点上。这些点承受着比其他部分更大的压力。 2. 断裂与能量释放:

脆性断裂: 意大利面条是脆性材料，这意味着它在受到足够大的应力时，不会发生明显的塑性变形，而是直接断裂。 能量储存与释放: 当我们弯曲意大利面条时，实际上是在对其进行弹性形变，并将能量储存在其中。当弯曲处的应力超过意大利面条的强度极限时，就会发生断裂。断裂时，储存的弹性势能迅速释放出来。 3. 碎屑的加速:

应力波: 断裂产生的应力波会沿着意大利面条传递，并到达末端。 能量传递: 这股应力波携带了之前储存的能量，传递给末端的碎屑。 高速喷射: 由于碎屑的质量很小，即使传递的能量不多，也能使其获得很高的速度，从而被高速喷射出去。 类似于鞭子的抽打效应，能量集中传递到鞭梢，使其速度很快。 4. 管道的约束作用:

限制运动方向: 管道限制了意大利面条的弯曲方式，迫使其只能沿着管道的形状弯曲。这可能导致应力更加集中。 提供支撑: 管道也为意大利面条提供了一定的支撑，防止其在弯曲过程中发生过度的形变，从而促使应力集中到特定点。 总结:

意大利面碎屑高速喷射的现象是多种因素共同作用的结果：

外力作用: 推动力是整个过程的驱动力。 材料特性: 意大利面条的脆性使其易于断裂。 结构特性: 弯曲的管道和意大利面条的几何形状导致应力集中。 能量释放: 断裂释放了之前储存的弹性势能，并传递给碎屑。 这个现象看似简单，但实际上包含了力学、材料学和能量传递等多方面的物理原理。通过分析，我们可以更好地理解其中的奥秘。

2.1.7. 视频和现象#

2025IYPT/CUPT 13.Spaghetti Accelerator第十三题 意大利面加速器

2025IYPT/CUPT 13.Spaghetti Accelerator第十三题 意大利面加速器

https://www.youtube.com/shorts/SDxQ9tpH_Jw

2.1.8. 细节解释#

chatgpt

2.1.9. 细节解释#

gemini

2.1.10. 细节解释#

deepseek

2.1.11. 细节解释#

qwen

2.1.12. 参考文献#

Audoly, B., & Neukirch, S. (2005). Fragmentation of rods by cascading cracks: Why spaghetti does not break in half.

The Fracture of Brittle Materials

材料力学

2.1.13. 实验设计#

2.1.13.1. 基本参数，抽样反复测量#

  • 测量杨氏模量

  • 测量截面惯量矩 \(\frac{\pi D^4}{64}\)

  • 质量、长度，直径

2.1.13.2. 实验设计#

  • 利用悬臂梁测量E(可参加实验竞赛)

  • 测量弯矩

  • 单独测量断裂最大挠度，估计断裂最大应变量

  • 单独测量短面条弯曲后弹射运动

  • 针对弯管进行测量

2.2. 基础理论#

2.2.1. 基本假设#

  • 连续

  • 均匀

  • 各项同性

2.2.2. 载荷和载荷集度#

  • 体载荷 \(N/m^3\)

  • 面载荷 \(N/m^2\)

  • 线载荷 \(N/m\)

  • 集中载荷 作用区域比较小

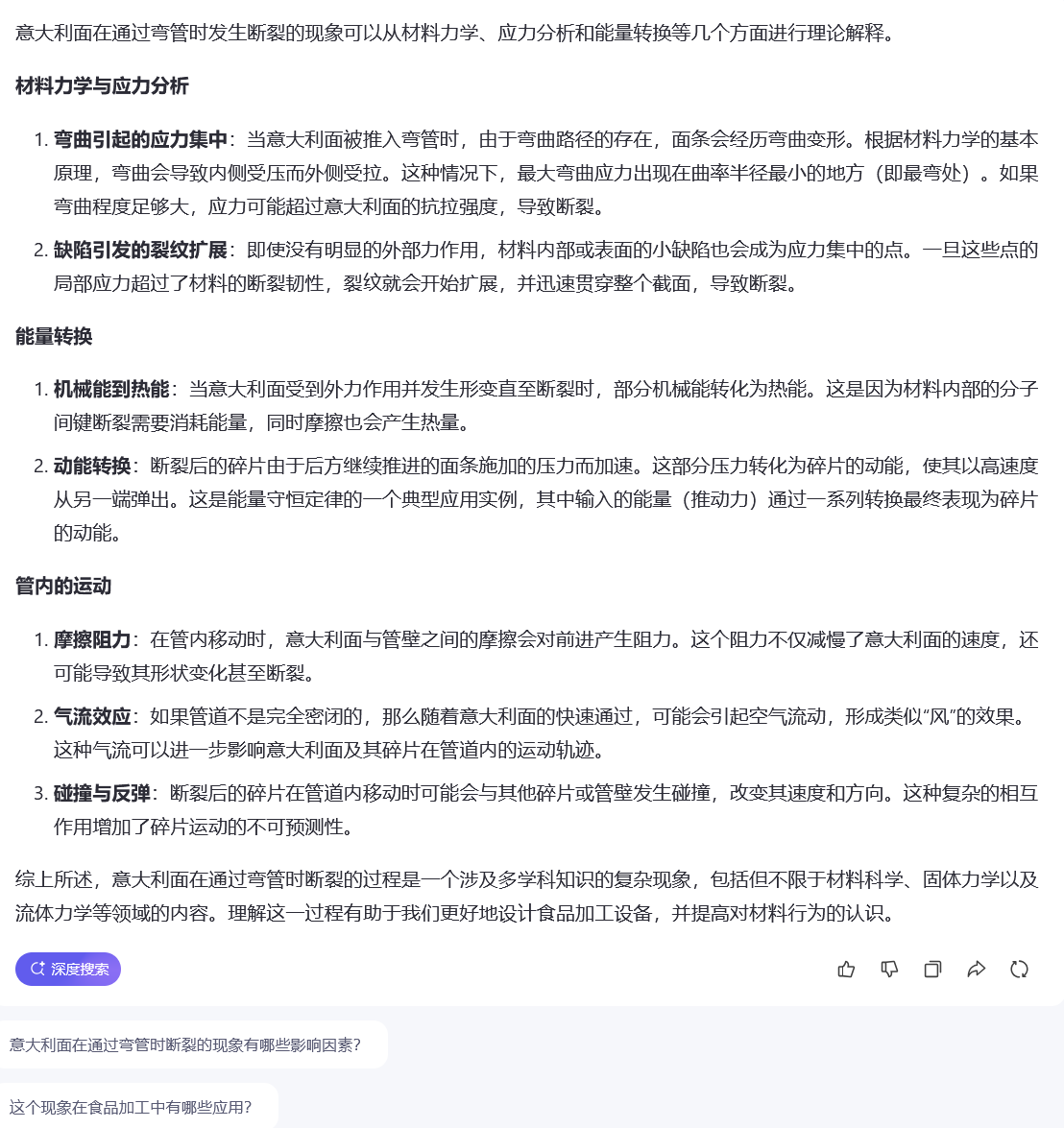
2.2.3. 内力#

构件在受外力作用而变形时，其内部各质点之间因相对位置改变而产生的相互作用力就是内力。这样的内力随外力的变化而变化，外力增大，内力也增大。

2.2.4. 应力#

  • 简单理解 $\(\vec{p}=\frac{\vec{F}}{S}\)$

  • 正应力和切应力

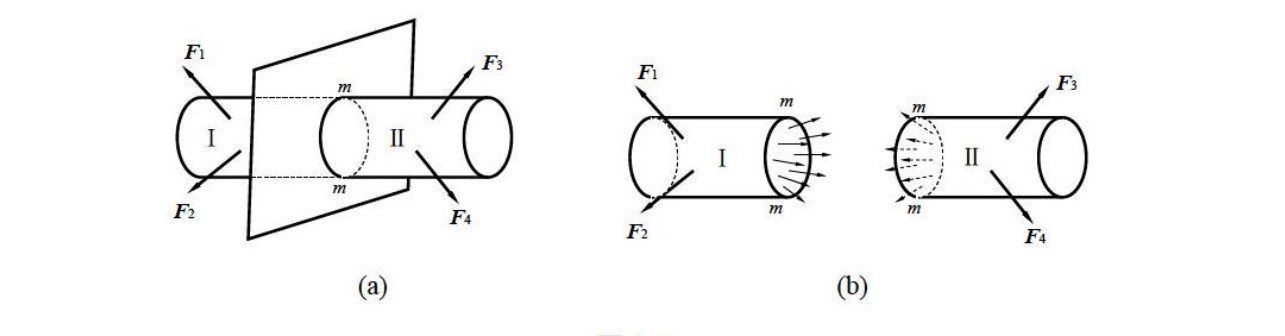
2.2.5. 变形与应变#

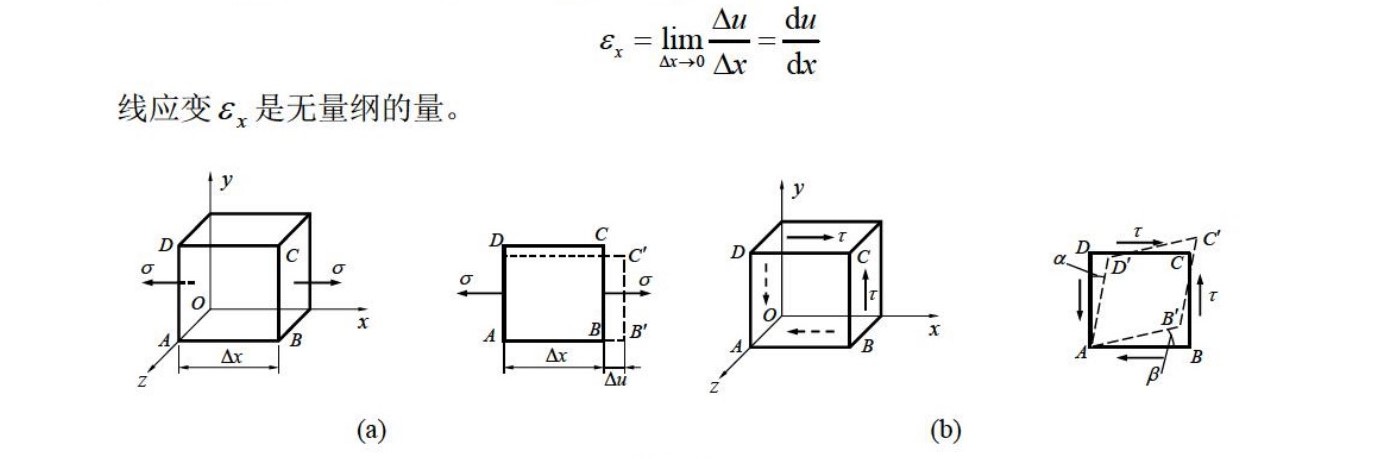
  • 正应变长度变

  • 切应变(剪应变)角度变

2.2.6. 杆件变形#

  • 拉伸压缩

  • 见应变

  • 扭转

  • 弯曲

杆在拉伸时，拉力方向(长度)发生线应变\(\epsilon=\frac{\delta l}{l}\)，杆会变细，横向（半径）也会发生应变\(\epsilon^{\prime}=\frac{\delta b}{b}\)

泊松比:

\[\mu=\frac{\epsilon^{\prime}}{\epsilon}\]

弹性模量，杨氏模量:

\[E=\frac{LF}{\Delta L A}\]
\[\sigma=\frac{F}{A}\]
\[\sigma=E\epsilon\]

应变能:

\[v_{\epsilon}=\frac{E\epsilon^2}{2}\]

  • 弹性阶段

  • 屈服阶段

  • 强化阶段 强度极限

  • 局部变形

  • 应力集中

2.2.7. 扭转和剪切#

切应变和力矩有关: $\(T=M_e\)$

切应力: $\(\tau=\frac{T}{2\pi r^2 \delta}\)\( 切应变: \)\(\gamma=\frac{r\phi}{l}\)$

\[\tau=G\gamma\]
\[G={\frac{E}{2(1+\mu)}}\]

2.2.8. 弯曲内力#

支反力: 固定位置的反作用力和力矩 弯矩:

2.2.9. 原理分析#

2.2.9.1. 前期弯曲#

2.2.9.1.1. 纯弯曲#

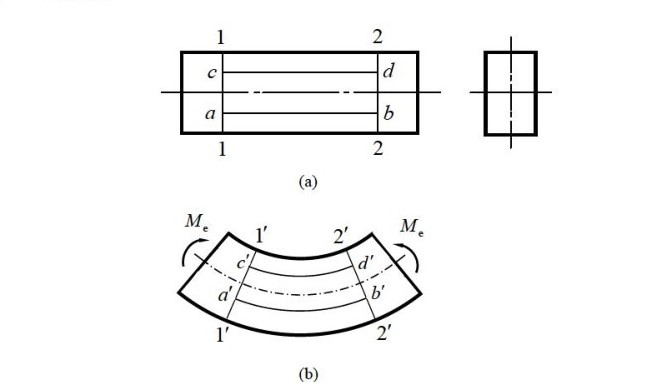
2.2.9.1.2. 弯矩#

2.2.9.1.3. 挠度#

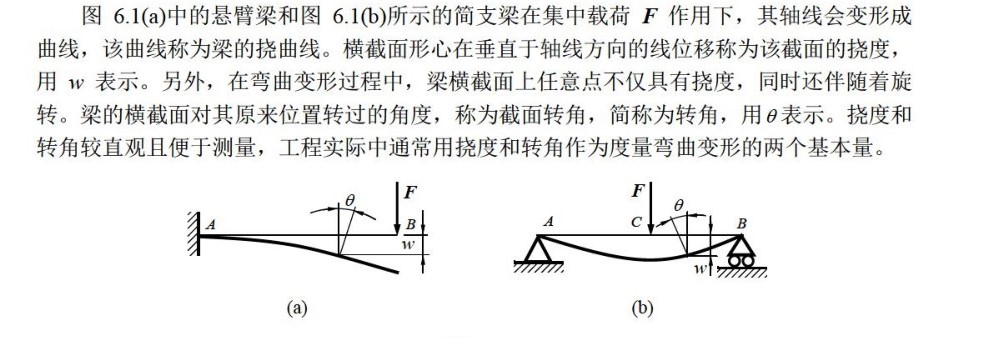
Tip

用来测量杨氏模量E

大挠度悬臂梁弯曲满足:

2.2.9.1.4. 能量#

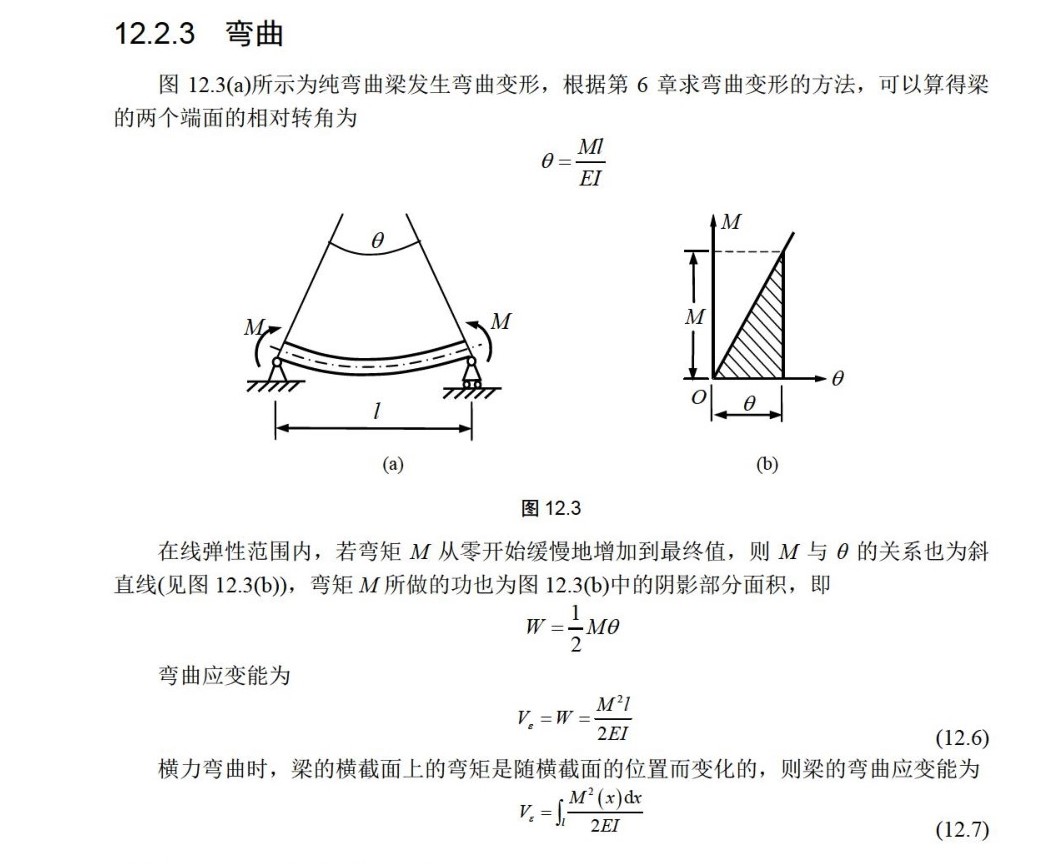
2.2.9.2. 中期断裂#

  • 难以分析，参考部分理论

2.2.9.3. 后期运动#

  • 弹性能量和重力势能转化为转动和平动

  • 简化为一端受力的刚体运动

Contents